arithm::ModPGrp Class Reference
Implements a q-subgroup of a modular field. More...
#include <modpgrp.hpp>
 Inheritance diagram for arithm::ModPGrp:
Inheritance diagram for arithm::ModPGrp: Collaboration diagram for arithm::ModPGrp:
Collaboration diagram for arithm::ModPGrp:Public Member Functions | |
| ModPGrp (mpz_class ord, mpz_class add, mpz_class gen, uint8_t encoding) | |
| Initializes a modular p-subgroup of order ord by building a new ModField instance of order add, setting it to be the baseGroup and using gen as a generator. | |
| ModPGrp (verifierUtils::ByteTree *bt) | |
| Parses a ByteTree to create a ModPGrp. | |
| verifierUtils::ByteTree * | toByteTree () |
| Returns the bytetree representation of this group. | |
| ArrayOfElmts | getRandArray (cryptoTools::PRG *prg, unsigned int nr, unsigned int n0) |
| Returns an array of elements of size n0 derived using a prg. | |
 Public Member Functions inherited from arithm::PSubGroup Public Member Functions inherited from arithm::PSubGroup | |
| PSubGroup (Group *bgrp, mpz_class order, mpz_class gen) | |
| Initializes a p-subgroup instance. | |
| Elmt | multiplication (Elmt e1, Elmt e2) |
| Returns the product of the two elements as an element of this group. | |
| Elmt | multInverse (Elmt e) |
Returns 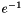 as an element of this group. as an element of this group. | |
| Elmt | exponentiation (Elmt e, Elmt s) |
Returns the 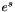 as an element of this group. as an element of this group. | |
| unsigned int | getLeafSize () |
| Returns the byte size the leaves representing element of this group must have. | |
| bool | isIn (mpz_class r) |
Returns true if and only if 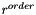 is equal to 1. is equal to 1. | |
| std::string | getType () |
| Returns a string containing the name of this Group. | |
 Public Member Functions inherited from arithm::Group Public Member Functions inherited from arithm::Group | |
| Group (mpz_class order, mpz_class gen) | |
| Sets the attributes of a new group instance. | |
| bool | compare (Elmt e1, Elmt e2) |
| Returns true if e1 and e2 have identical values, false otherwise. | |
| ArrayOfElmts | multiplication (ArrayOfElmts e1, ArrayOfElmts e2) |
Returns 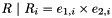 as an array of elements of this group. as an array of elements of this group. | |
| ArrayOfElmts | multInverse (ArrayOfElmts e) |
Returns 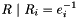 as an array of elements of this group. as an array of elements of this group. | |
| ArrayOfElmts | exponentiation (ArrayOfElmts e, ArrayOfElmts s) |
Returns 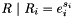 as an array of elements of this group. as an array of elements of this group. | |
| Elmt | product (ArrayOfElmts e) |
Returns 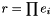 as an element of this group. as an element of this group. | |
| Elmt | expProduct (ArrayOfElmts e, ArrayOfElmts s) |
Returns 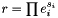 as an element of this group. as an element of this group. | |
| bool | compare (ArrayOfElmts e1, ArrayOfElmts e2) |
| Returns true if e1 and e2 have identical values component-wise, false if at least one of the component is different. | |
| virtual Elmt | encode (std::vector< uint8_t > message) |
| Encodes the message into a element of this group. | |
| virtual std::vector< uint8_t > | decode (Elmt e) |
| Returns the element encoded in the element given as a paramater. | |
| Elmt | getOne () |
| Returns an element containing the unit of this group. | |
| ArrayOfElmts | getOne (unsigned int n) |
| Returns an array containing n copies of the unit of this group. | |
| Elmt | getElmt (mpz_class repr) |
| Returns the element of this group which has repr as a representative. | |
| Elmt | getElmt (verifierUtils::ByteTree *bt) |
| Returns the element of this group which bt as a bytetree representation. | |
| ArrayOfElmts | getArray (verifierUtils::ByteTree *bt) |
| Returns the array of elements of this group which has bt as a bytetree representation. | |
| mpz_class | getMultOrder () |
| Returns the multiplicative generator of this group. | |
| Elmt | getGenerator () |
| Returns the multiplicative generator of this group as an element of this group. | |
| ArrayOfElmts | getGenerator (unsigned int n) |
| Returns an array containing n copies of the multiplicative order of this group. | |
Private Attributes | |
| uint8_t | code |
| The type of encoding to use to parse and store messages using Elmts of this group. | |
| mpz_class | addOrder |
| The additive order of the base ModField. | |
Additional Inherited Members | |
 Protected Attributes inherited from arithm::PSubGroup Protected Attributes inherited from arithm::PSubGroup | |
| Group * | baseGroup |
| The group this instance is a p-subgroup of. | |
| mpz_class | coOrder |
| The order of baseGroup divided by that of this one. | |
Detailed Description
Implements a q-subgroup of a modular field.
Definition at line 23 of file modpgrp.hpp.
Constructor & Destructor Documentation
| ModPGrp::ModPGrp | ( | mpz_class | ord, |
| mpz_class | add, | ||
| mpz_class | gen, | ||
| uint8_t | encoding | ||
| ) |
| ModPGrp::ModPGrp | ( | verifierUtils::ByteTree * | bt | ) |
Parses a ByteTree to create a ModPGrp.
- Parameters
-
bt A Node containing 4 leaves: - the additive order
- the order of this subgroup
- the generator
- the encoding to use
Definition at line 27 of file modpgrp.cpp.
:
{
if (!bt->isNode())
{
std::cout<<"ERROR: in ModPGrp(bt), bt is not a node. "
<<"\nbt=";
bt->prettyPrint("");
std::cout<<std::endl;
exit(1);
}
}



