Implements a p-subgroup (as defined in Sylow theory) of any multiplicative group. More...
#include <psubgroup.hpp>
 Inheritance diagram for arithm::PSubGroup:
Inheritance diagram for arithm::PSubGroup: Collaboration diagram for arithm::PSubGroup:
Collaboration diagram for arithm::PSubGroup:Public Member Functions | |
| PSubGroup (Group *bgrp, mpz_class order, mpz_class gen) | |
| Initializes a p-subgroup instance. | |
| Elmt | multiplication (Elmt e1, Elmt e2) |
| Returns the product of the two elements as an element of this group. | |
| Elmt | multInverse (Elmt e) |
Returns 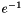 as an element of this group. as an element of this group. | |
| Elmt | exponentiation (Elmt e, Elmt s) |
Returns the 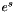 as an element of this group. as an element of this group. | |
| unsigned int | getLeafSize () |
| Returns the byte size the leaves representing element of this group must have. | |
| bool | isIn (mpz_class r) |
Returns true if and only if 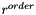 is equal to 1. is equal to 1. | |
| std::string | getType () |
| Returns a string containing the name of this Group. | |
 Public Member Functions inherited from arithm::Group Public Member Functions inherited from arithm::Group | |
| Group (mpz_class order, mpz_class gen) | |
| Sets the attributes of a new group instance. | |
| virtual verifierUtils::ByteTree * | toByteTree () |
| Returns the bytetree representation of this group. | |
| bool | compare (Elmt e1, Elmt e2) |
| Returns true if e1 and e2 have identical values, false otherwise. | |
| ArrayOfElmts | multiplication (ArrayOfElmts e1, ArrayOfElmts e2) |
Returns 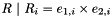 as an array of elements of this group. as an array of elements of this group. | |
| ArrayOfElmts | multInverse (ArrayOfElmts e) |
Returns 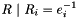 as an array of elements of this group. as an array of elements of this group. | |
| ArrayOfElmts | exponentiation (ArrayOfElmts e, ArrayOfElmts s) |
Returns 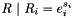 as an array of elements of this group. as an array of elements of this group. | |
| Elmt | product (ArrayOfElmts e) |
Returns 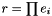 as an element of this group. as an element of this group. | |
| Elmt | expProduct (ArrayOfElmts e, ArrayOfElmts s) |
Returns 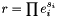 as an element of this group. as an element of this group. | |
| bool | compare (ArrayOfElmts e1, ArrayOfElmts e2) |
| Returns true if e1 and e2 have identical values component-wise, false if at least one of the component is different. | |
| virtual Elmt | encode (std::vector< uint8_t > message) |
| Encodes the message into a element of this group. | |
| virtual std::vector< uint8_t > | decode (Elmt e) |
| Returns the element encoded in the element given as a paramater. | |
| Elmt | getOne () |
| Returns an element containing the unit of this group. | |
| ArrayOfElmts | getOne (unsigned int n) |
| Returns an array containing n copies of the unit of this group. | |
| Elmt | getElmt (mpz_class repr) |
| Returns the element of this group which has repr as a representative. | |
| Elmt | getElmt (verifierUtils::ByteTree *bt) |
| Returns the element of this group which bt as a bytetree representation. | |
| ArrayOfElmts | getArray (verifierUtils::ByteTree *bt) |
| Returns the array of elements of this group which has bt as a bytetree representation. | |
| virtual ArrayOfElmts | getRandArray (cryptoTools::PRG *prg, unsigned int nr, unsigned int n0) |
| Returns an array of elements of size n0 derived using a prg. | |
| mpz_class | getMultOrder () |
| Returns the multiplicative generator of this group. | |
| Elmt | getGenerator () |
| Returns the multiplicative generator of this group as an element of this group. | |
| ArrayOfElmts | getGenerator (unsigned int n) |
| Returns an array containing n copies of the multiplicative order of this group. | |
Protected Attributes | |
| Group * | baseGroup |
| The group this instance is a p-subgroup of. | |
| mpz_class | coOrder |
| The order of baseGroup divided by that of this one. | |
 Protected Attributes inherited from arithm::Group Protected Attributes inherited from arithm::Group | |
| mpz_class | multOrder |
| The order of this multiplicative group. | |
| mpz_class | generator |
| The generator to use for this group. | |
Detailed Description
Implements a p-subgroup (as defined in Sylow theory) of any multiplicative group.
Definition at line 26 of file psubgroup.hpp.
Constructor & Destructor Documentation
| PSubGroup::PSubGroup | ( | Group * | bgrp, |
| mpz_class | order, | ||
| mpz_class | gen | ||
| ) |
Initializes a p-subgroup instance.
- Parameters
-
bgrp The group this instance is a subgroup of. order The order of this subgroup. gen A generator of this subgroup.
Definition at line 18 of file psubgroup.cpp.
Member Function Documentation
Returns the 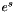 as an element of this group.
as an element of this group.
Reimplemented from arithm::Group.
Definition at line 45 of file psubgroup.cpp.
|
virtual |
Returns the byte size the leaves representing element of this group must have.
Reimplemented from arithm::Group.
Definition at line 51 of file psubgroup.cpp.
|
virtual |
Returns a string containing the name of this Group.
Reimplemented from arithm::Group.
Definition at line 65 of file psubgroup.cpp.
|
virtual |
Returns true if and only if 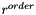 is equal to 1.
is equal to 1.
Reimplemented from arithm::Group.
Definition at line 57 of file psubgroup.cpp.
Returns 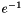 as an element of this group.
as an element of this group.
Reimplemented from arithm::Group.
Definition at line 39 of file psubgroup.cpp.
Returns the product of the two elements as an element of this group.
Reimplemented from arithm::Group.
Definition at line 33 of file psubgroup.cpp.
Member Data Documentation
|
protected |
The group this instance is a p-subgroup of.
Definition at line 32 of file psubgroup.hpp.
|
protected |
The order of baseGroup divided by that of this one.
Definition at line 37 of file psubgroup.hpp.
The documentation for this class was generated from the following files:
- arithm/psubgroup/psubgroup.hpp
- arithm/psubgroup/psubgroup.cpp




