Models a mathematical field with a given additive order, multiplicative order, addition, multiplication, unit and zero. More...
#include <field.hpp>
 Inheritance diagram for arithm::Field:
Inheritance diagram for arithm::Field: Collaboration diagram for arithm::Field:
Collaboration diagram for arithm::Field:Public Member Functions | |
| Field (mpz_class aOrder) | |
| Constructs a Field instance by setting only the value of addOrder, generator and multOrder being set to 1 and 0. | |
| Field (mpz_class aOrder, mpz_class mOrder, mpz_class gen) | |
| Constructs a Field instance by setting the values of addOrder, multOrder and generator. | |
Additive element operations | |
| virtual Elmt | addition (Elmt e1, Elmt e2) |
Returns  as an element of this field. as an element of this field. | |
| virtual Elmt | addInverse (Elmt e) |
Returns 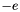 as an element of the field. as an element of the field. | |
Additive array operations | |
| ArrayOfElmts | addition (ArrayOfElmts e1, ArrayOfElmts e2) |
Returns 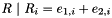 . If the sizes mismatch, exits with exitcode 1. . If the sizes mismatch, exits with exitcode 1. | |
| ArrayOfElmts | addInverse (ArrayOfElmts a) |
Returns 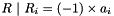 as an array of elements of this field. as an array of elements of this field. | |
| Elmt | sum (ArrayOfElmts a) |
Returns 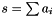 as an element of this field. as an element of this field. | |
Obtaining field elements | |
| Elmt | getZero () |
| Returns the neutral element for addition. | |
| ArrayOfElmts | getZero (unsigned int n) |
| Returns an array of field elements containging n copies of the neutral element for addition. | |
Data about the field. | |
| mpz_class | getAddOrder () |
| unsigned int | getLeafSize () |
| Returns the byte size the leaves representing element of this group must have. | |
| virtual std::string | getType () |
| Returns a string containing the name of this Group. | |
 Public Member Functions inherited from arithm::Group Public Member Functions inherited from arithm::Group | |
| Group (mpz_class order, mpz_class gen) | |
| Sets the attributes of a new group instance. | |
| virtual verifierUtils::ByteTree * | toByteTree () |
| Returns the bytetree representation of this group. | |
| virtual Elmt | multiplication (Elmt e1, Elmt e2) |
| Returns the product of the two elements as an element of this group. | |
| virtual Elmt | multInverse (Elmt e) |
Returns 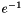 as an element of this group. as an element of this group. | |
| virtual Elmt | exponentiation (Elmt e, Elmt s) |
Returns the 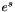 as an element of this group. as an element of this group. | |
| bool | compare (Elmt e1, Elmt e2) |
| Returns true if e1 and e2 have identical values, false otherwise. | |
| ArrayOfElmts | multiplication (ArrayOfElmts e1, ArrayOfElmts e2) |
Returns 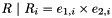 as an array of elements of this group. as an array of elements of this group. | |
| ArrayOfElmts | multInverse (ArrayOfElmts e) |
Returns 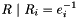 as an array of elements of this group. as an array of elements of this group. | |
| ArrayOfElmts | exponentiation (ArrayOfElmts e, ArrayOfElmts s) |
Returns 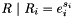 as an array of elements of this group. as an array of elements of this group. | |
| Elmt | product (ArrayOfElmts e) |
Returns 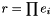 as an element of this group. as an element of this group. | |
| Elmt | expProduct (ArrayOfElmts e, ArrayOfElmts s) |
Returns 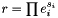 as an element of this group. as an element of this group. | |
| bool | compare (ArrayOfElmts e1, ArrayOfElmts e2) |
| Returns true if e1 and e2 have identical values component-wise, false if at least one of the component is different. | |
| virtual Elmt | encode (std::vector< uint8_t > message) |
| Encodes the message into a element of this group. | |
| virtual std::vector< uint8_t > | decode (Elmt e) |
| Returns the element encoded in the element given as a paramater. | |
| Elmt | getOne () |
| Returns an element containing the unit of this group. | |
| ArrayOfElmts | getOne (unsigned int n) |
| Returns an array containing n copies of the unit of this group. | |
| Elmt | getElmt (mpz_class repr) |
| Returns the element of this group which has repr as a representative. | |
| Elmt | getElmt (verifierUtils::ByteTree *bt) |
| Returns the element of this group which bt as a bytetree representation. | |
| ArrayOfElmts | getArray (verifierUtils::ByteTree *bt) |
| Returns the array of elements of this group which has bt as a bytetree representation. | |
| virtual ArrayOfElmts | getRandArray (cryptoTools::PRG *prg, unsigned int nr, unsigned int n0) |
| Returns an array of elements of size n0 derived using a prg. | |
| mpz_class | getMultOrder () |
| Returns the multiplicative generator of this group. | |
| Elmt | getGenerator () |
| Returns the multiplicative generator of this group as an element of this group. | |
| ArrayOfElmts | getGenerator (unsigned int n) |
| Returns an array containing n copies of the multiplicative order of this group. | |
| virtual bool | isIn (mpz_class repr) |
| Returns true if the element of representative repr is in this group. | |
Protected Attributes | |
| mpz_class | addOrder |
| The additive order (characteristic) of the field. | |
 Protected Attributes inherited from arithm::Group Protected Attributes inherited from arithm::Group | |
| mpz_class | multOrder |
| The order of this multiplicative group. | |
| mpz_class | generator |
| The generator to use for this group. | |
Detailed Description
Models a mathematical field with a given additive order, multiplicative order, addition, multiplication, unit and zero.
It is a virtual class providing an interface that has to be implemented by every field used in verificatum.
Constructor & Destructor Documentation
| Field::Field | ( | mpz_class | aOrder | ) |
Member Function Documentation
Returns 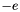 as an element of the field.
as an element of the field.
Reimplemented in arithm::ModField.
| ArrayOfElmts Field::addInverse | ( | ArrayOfElmts | a | ) |
Returns 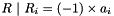 as an array of elements of this field.
as an array of elements of this field.
Returns  as an element of this field.
as an element of this field.
Reimplemented in arithm::ModField.
| ArrayOfElmts Field::addition | ( | ArrayOfElmts | e1, |
| ArrayOfElmts | e2 | ||
| ) |
Returns 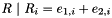 . If the sizes mismatch, exits with exitcode 1.
. If the sizes mismatch, exits with exitcode 1.
Definition at line 53 of file field.cpp.
| mpz_class Field::getAddOrder | ( | ) |
|
virtual |
Returns the byte size the leaves representing element of this group must have.
Reimplemented from arithm::Group.
|
virtual |
Returns a string containing the name of this Group.
Reimplemented from arithm::Group.
Reimplemented in arithm::ModField.
Definition at line 126 of file field.cpp.
| Elmt Field::getZero | ( | ) |
| ArrayOfElmts Field::getZero | ( | unsigned int | n | ) |
Returns an array of field elements containging n copies of the neutral element for addition.
| Elmt Field::sum | ( | ArrayOfElmts | a | ) |
Member Data Documentation
|
protected |
The documentation for this class was generated from the following files:




